Sun Drives Weather

Reinhold Koch

2024-02-07

Background

The National Oceanic and Atmospheric Administration publishes freely accessible daily climate data from thousands of weather stations in the world.

I wondered how much daily average temperature in each station can be explained by solar irradiation alone.

It also peeked my interest how well statistical linear models could handle the amount of data from meteorology.

Let’s see!

Data

years <- as.character(2023:2023)
for (year in years[!file.exists(years)]) {
  tf <- tempfile('climate', fileext = '.tar.gz')
  download.file(url = paste0('https://www.ncei.noaa.gov/data/global-summary-of-the-day/archive/',
                             year, '.tar.gz'),
                destfile = tf)
  untar(tf, exdir = year)
}
# col_date(format='%F')
coltypes <- readr::cols_only(STATION='c',
                        DATE=readr::col_date(format = '%F'),
                        LATITUDE='d',
                        LONGITUDE='d',
                        ELEVATION='d',
                        NAME='c',
                        TEMP='d')

dat0 <- dplyr::bind_rows(lapply(list.files(path=years, full.names = TRUE),
                               readr::read_csv, col_types=coltypes))

peek into data

print(dat0, n=10, width=70)
# A tibble: 4,038,747 × 7
   STATION     DATE       LATITUDE LONGITUDE ELEVATION NAME       TEMP
   <chr>       <date>        <dbl>     <dbl>     <dbl> <chr>     <dbl>
 1 01001099999 2023-01-01     70.9     -8.67         9 JAN MAYE…  18.1
 2 01001099999 2023-01-02     70.9     -8.67         9 JAN MAYE…  25.8
 3 01001099999 2023-01-03     70.9     -8.67         9 JAN MAYE…  35.8
 4 01001099999 2023-01-04     70.9     -8.67         9 JAN MAYE…  37  
 5 01001099999 2023-01-05     70.9     -8.67         9 JAN MAYE…  35.4
 6 01001099999 2023-01-06     70.9     -8.67         9 JAN MAYE…  32.7
 7 01001099999 2023-01-07     70.9     -8.67         9 JAN MAYE…  34.7
 8 01001099999 2023-01-08     70.9     -8.67         9 JAN MAYE…  35.2
 9 01001099999 2023-01-09     70.9     -8.67         9 JAN MAYE…  34  
10 01001099999 2023-01-10     70.9     -8.67         9 JAN MAYE…  31.6
# ℹ 4,038,737 more rows

data quality

summary(dat0)
   STATION               DATE               LATITUDE        LONGITUDE       
 Length:4038747     Min.   :2023-01-01   Min.   :-90.00   Min.   :-179.983  
 Class :character   1st Qu.:2023-04-01   1st Qu.: 23.84   1st Qu.: -82.454  
 Mode  :character   Median :2023-07-02   Median : 40.08   Median :   8.517  
                    Mean   :2023-07-01   Mean   : 31.66   Mean   :  -1.280  
                    3rd Qu.:2023-10-02   3rd Qu.: 49.22   3rd Qu.:  64.230  
                    Max.   :2023-12-31   Max.   : 83.65   Max.   : 179.500  
                                         NA's   :13408    NA's   :13408     
   ELEVATION          NAME                TEMP        
 Min.   :-999.9   Length:4038747     Min.   :-114.30  
 1st Qu.:  31.0   Class :character   1st Qu.:  42.70  
 Median : 155.1   Mode  :character   Median :  59.70  
 Mean   : 361.8                      Mean   :  56.49  
 3rd Qu.: 446.2                      3rd Qu.:  74.10  
 Max.   :4701.0                      Max.   : 110.00  
 NA's   :13770

“-999.9” as missing elevation and other fixes

dat0$ELEVATION <- ifelse(dat0$ELEVATION == -999.9, NA, dat0$ELEVATION)

convert temperature to Celsius and elevation to km (for numerical reasons)

dat0$ELEVATION <- dat0$ELEVATION/1000
dat0$TEMP <- (dat0$TEMP-32)*5/9

how many observations per station?

tail(table(table(dat0$STATION)), n=15)

 351  352  353  354  355  356  357  358  359  360  361  362  363  364  365 
  63  111  171  102   75  100   99   86  117  151  220  354  459  702 6032

About half of the stations have an observation for each day in 2023.
Let’s concentrate on the stations with at least 360 observations -

and remove all stations with missing coordinates.

base data

nrecords <- dat0 |>
  dplyr::group_by(STATION) |> tally()
dat1 <- dat0 |> 
  dplyr::filter(!is.na(LATITUDE) & !is.na(LONGITUDE) & !is.na(ELEVATION) & STATION %in% 
                  subset(nrecords, n>=360)$STATION)

This data now provides my base for investigation.

functions for insolation and maximum sun elevation

From Jean Meeus’ book “Astronomical Algorithms” good approximations for solar irradiation per day and maximum sun elevation can be computed - see code for details.

# sun declination
declination <- function(J2000T) asin(sin(epsilon(J2000T)) * sin(lambda(J2000T)))

# irradiation in kWh per m^2 per day
insolation <- function(J2000T, latitude) {
  rho <- rho(J2000T)
  h0 <- h0(J2000T, latitude)
  x <- sin(epsilon(J2000T)) * sin(lambda(J2000T))
  10.4033856721 * rho*rho * (h0*sin(latitude)*x + cos(latitude)*cos(asin(x))*sin(h0))
}

add sun parameters to dataframe

With astronomical functions in place I can compute for each observation the daily sun irradiation energy per m^2 and the sine of maximum sun elevation.

dat <- dat1 |>
  dplyr::group_by(STATION) |>
  dplyr::mutate(
    insolation=insolation(J2000_cent(as.POSIXct(DATE)+43200), pi*LATITUDE/180),
    delta_sol= ifelse(DATE==lag(DATE)+1, 100*(insolation-lag(insolation)), NA),
    maxsun = cos(pi*LATITUDE/180-declination(J2000_cent(as.POSIXct(DATE)+43200))),
    delta_maxsun=ifelse(DATE==lag(DATE)+1, 100*(maxsun-lag(maxsun)), NA)) |> 
  ungroup() |> 
  dplyr::filter(!is.na(delta_sol), !is.na(delta_maxsun))

sun parameters at diffent latitudes

ggplot(subset(dat, STATION %in% c('01001099999', '64450099999', '40192199999')),
       aes(x=DATE, y=maxsun)) + geom_point(color='green') + 
  geom_point(color='blue', aes(y=insolation/10)) +
  facet_wrap(~LATITUDE) + geom_point(color='black', aes(y=TEMP/15))

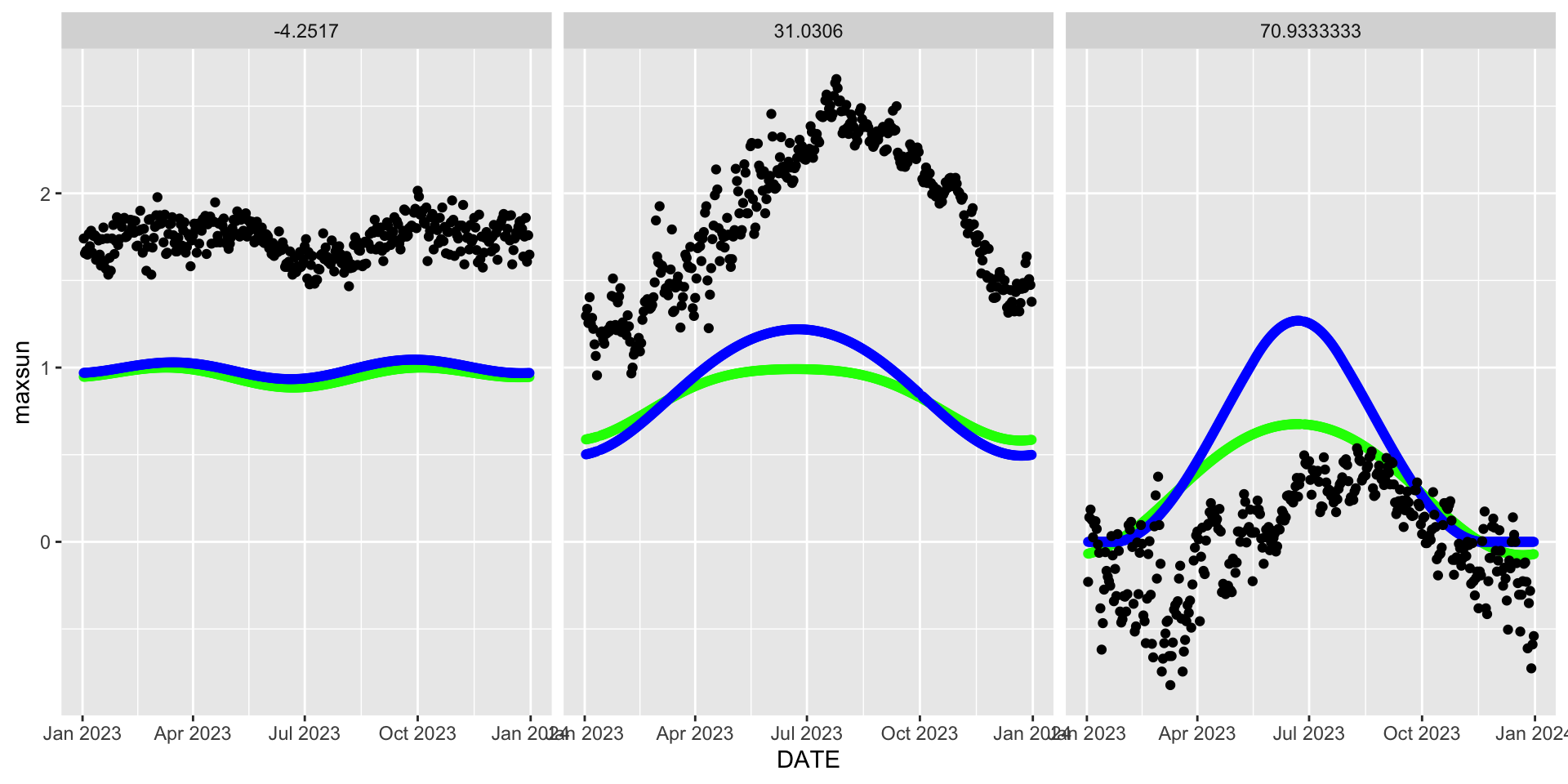
a parsimonious mixed effect model

m0 <- lme4::lmer(TEMP ~ ELEVATION + insolation * delta_maxsun + (delta_maxsun|STATION),
                 data=dat)
summary(m0)
Linear mixed model fit by REML ['lmerMod']
Formula: TEMP ~ ELEVATION + insolation * delta_maxsun + (delta_maxsun |  
    STATION)
   Data: dat

REML criterion at convergence: 16761814

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-13.5352  -0.5366   0.0216   0.5887   6.3420 

Random effects:
 Groups   Name         Variance Std.Dev. Corr
 STATION  (Intercept)  41.38    6.433        
          delta_maxsun 31.36    5.600    0.75
 Residual              19.75    4.444        
Number of obs: 2866271, groups:  STATION, 7894

Fixed effects:
                          Estimate Std. Error t value
(Intercept)             -1.3189055  0.0799846  -16.49
ELEVATION               -2.6139726  0.1041290  -25.10
insolation               2.0087287  0.0008365 2401.31
delta_maxsun            -0.7451291  0.0679113  -10.97
insolation:delta_maxsun -1.2813487  0.0034485 -371.56

Correlation of Fixed Effects:
            (Intr) ELEVAT insltn dlt_mx
ELEVATION   -0.416                     
insolation  -0.081 -0.002              
delta_maxsn  0.627 -0.001 -0.004       
insltn:dlt_ -0.003  0.005  0.009 -0.342

deal with phase lag of sun and temperature

dat$pred <- predict(m0)
ggplot(subset(dat, STATION %in% c('01001099999', '64450099999', '40192199999')),
aes(x=DATE, y=TEMP)) + geom_point() +
facet_wrap(~LATITUDE) + geom_point(color='green', aes(y=pred))

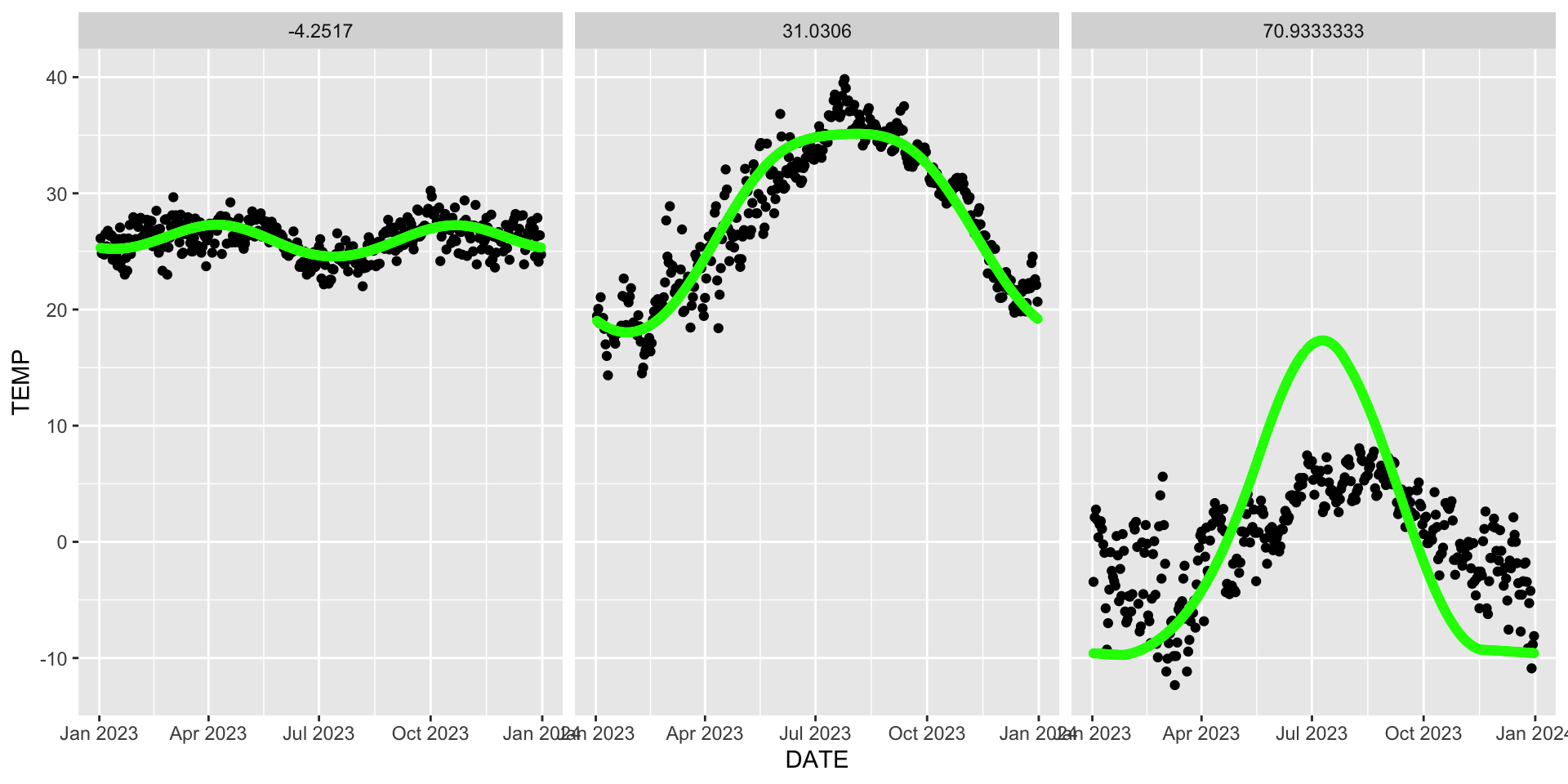
station specifics

stations <- dat[, c('STATION', 'LATITUDE', 'LONGITUDE', 'NAME')] |> 
  dplyr::group_by(STATION) |> 
  dplyr::slice_tail(n=1) |> 
  dplyr::left_join(tibble::rownames_to_column(lme4::ranef(m0)$STATION, var='STATION')) |> 
  ungroup()

station plot

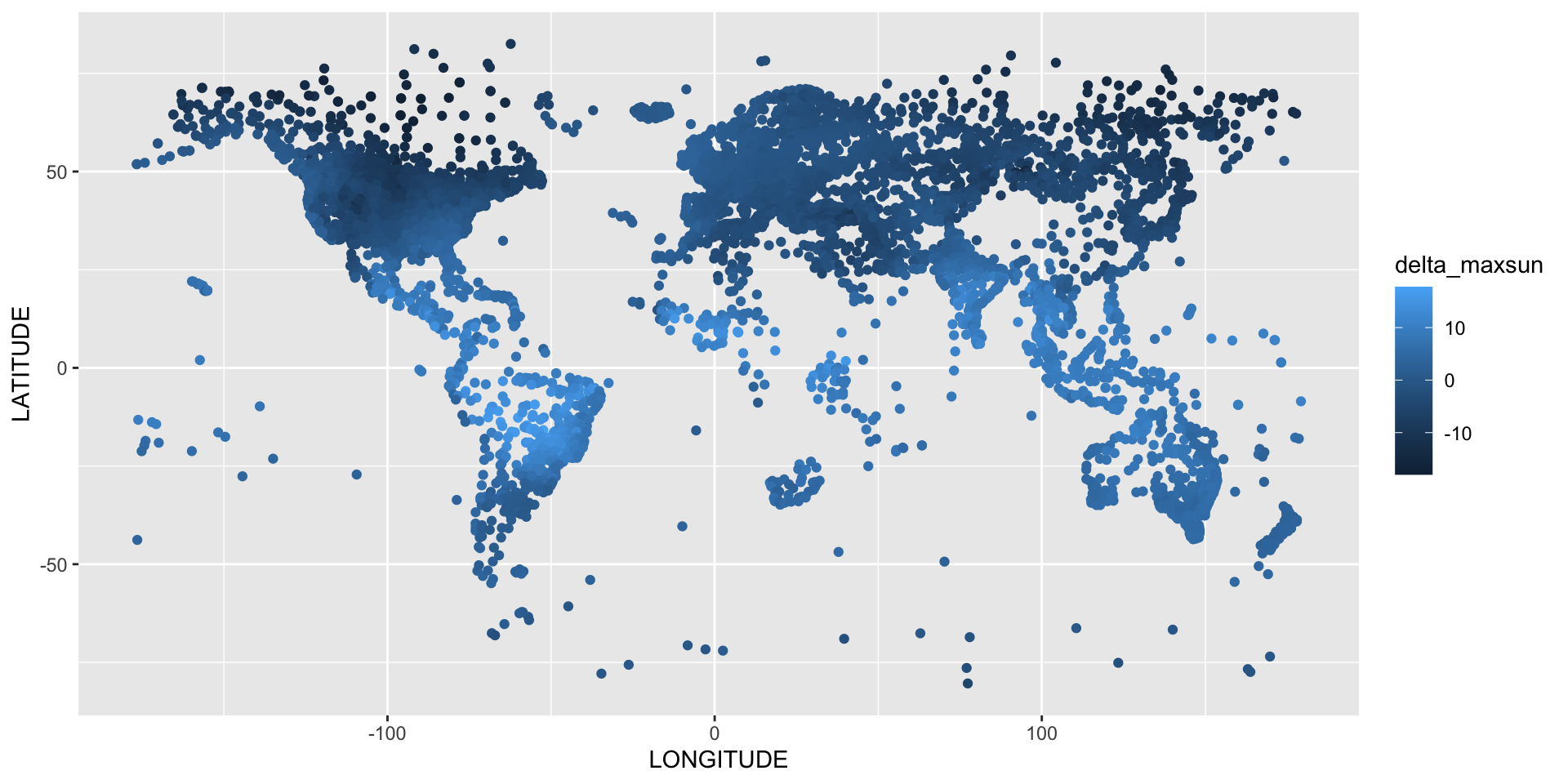
ggplot(data=stations, aes(x=LONGITUDE, y=LATITUDE, color=delta_maxsun)) + geom_point()

source in https://github.com/BaselDataScience/baseldatascience.github.io/blob/main/posts/sun_weather.qmd